uni memo

Tags uni's GitHub repo dashboard for blog analytics

juliaでjulia集合のプロットとアニメーション

| 4 min read | programming mandelbrot julia

juliaでjulia集合を作成した。ついでにmandelbrot集合も。配列系の演算子（.など）の勉強になった

環境

  • julia: 1.4.1
  • Plots: 1.5.9

mantelbrot集合

$$ z_{n+1} = z^2_{n}+c \\ z_{0} = 0 $$

として漸化式をとく

cは複素数なので実数a,bより以下のように表せる

$$c = a + ib$$

このとき $z \neq \infty$ となるcの集まりをmantelbrot集合という

zを実数(x,y)からなる$z=x+iy$として表現すると以下のように計算できる

$$ z_{n+1} = (x_n+iy_n)^2 + c \\ (x_n+iy_n)^2 + c = x_n^2 + 2ix_ny_n -y^2_n + a + ib $$

$z_{n+1} = x_{n+1} + iy_{n+1}$より実部と虚部を分ける

$$ x_{n+1} = x_n^2 - y^2_n + a \\ y_{n+1} = 2x_ny_n + b $$

実装

虚部を使用して計算

  • パッケージと関数
# install package
using Pkg
Pkg.add("Plots")
using Plots
 
function mandelbrot(c, n=2000)
    z = zero(c)
    for i = 1:n
        z = z^2 + c
        abs2(z) > 4 && return i
    end
    return n
end
  • plot
# plot
x = range(-2, 1; length=300)
y = range(-1.5, 1.5; length=300)
c = x' .+ y * im
 
r = mandelbrot.(c, 300)
heatmap(x, y, log10.(r),
    colorbar=false, size=(300, 300), color=reverse(cgrad(:jet1)))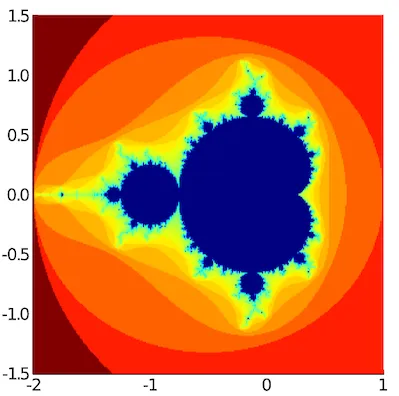

mandelbrot set

  • アニメーション
# 始点
xs = -1.45
ys = 0
t = range(0.01, 4, length=200)
ss = @. exp(-2*t)
anim = @animate for s in ss
    x = range(xs-s, xs+s, length=300)
    y = range(ys-s, ys+s, length=300)
    c = x' .+ y * im
    r = mandelbrot.(c, 300)
 
    # title
    s = @sprintf "x=%.3f~%.3f, y=%.3f~%.3f" xs-s xs+s ys-s ys+s;
    plot(x, y,label=s, size=(250,250))  
    heatmap!(x, y, log.(r),
        colorbar=false, size=(300, 300), color=reverse(cgrad(:jet1)))
end
gif(anim, fps=40, "mandelbrot.gif")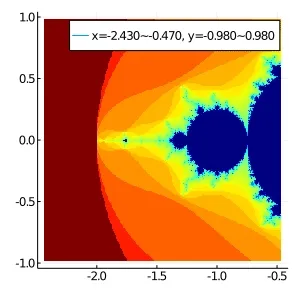

mandelbrot set

julia集合

mandelbrotと同じ漸化式を用いる。初期値と変化させる値が異なる

$c = a + ib$の（a,b)を変化させる

$z \neq \infty$となる$z_n$の集まりをjulia集合という

以下の初期値についてx, y, cを代入して求めていく

$$z_n = x_n + iy_n + c$$

実装

  • パッケージと関数
# install package
using Pkg
Pkg.add("Plots")
using Plots
 
function julia(c, z, n=2000)
    for i = 1:n
        z = z^2 + c
        abs2(z) > 4 && return i
    end
    return n
end
  • plot
x = range(-1.5, 1.5; length=600)
y = range(-1.25, 1.25; length=400)
a = -0.3
b = -0.63
c = complex(a, b)
 
r = @.julia(c, complex(x', y), 400)
heatmap(x, y, log10.(r),
    colorbar=false, size=(300, 300), color=:jet1)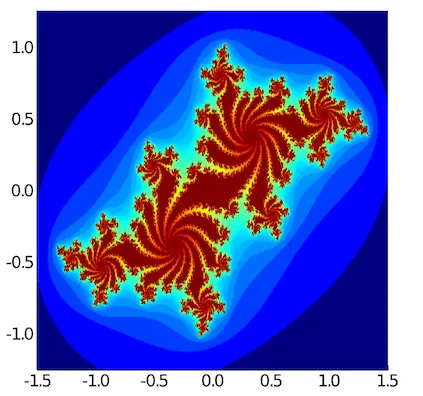

julia set

  • アニメーション
x = range(-1.5, 1.5; length=300)
y = range(-1.25, 1.25; length=300)
a = -0.7
@time anim = @animate for s in 0.5:-0.0025:0.27
    #a = s
    b = s
    c = complex(a, b)
    r = @.julia(c, complex(x', y), 600)
    s = @sprintf "a=%.3f, b=%.3f" a b;
    plot(x, y,label=s,size=(250,250))
    heatmap!(x, y, log10.(r),
        colorbar=false, size=(300, 300), color=:jet1)
end
 
gif(anim, "julia_set.gif", fps=40)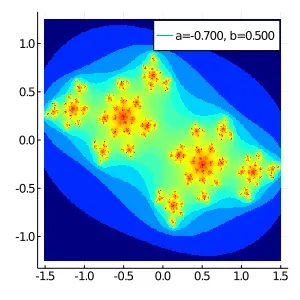

julia set

演算子

気になったところのメモ

  • 式の定義の前に@.をつけると全ての演算子が.形式に置換される

Mathematical Operations and Elementary Functions · The Julia Languageより

Furthermore, “dotted” updating operators like a .+= b (or @. a += b) are parsed as a .= a .+ b, where .= is a fused in-place assignment operation (see the dot syntax documentation).

参考