Search by

    uni farm

    pythonでニューラルネットワークを使った相転移検出 - イジングモデルのシミュレーション、CNNで学習 -

    programmingcolaboratoryphysicsising-modeltensorflow

    “ディープラーニングと物理学”本にイジングモデルのシミュレーション結果を機械学習モデルの学習データとして用いて、 ある状態が相転移状態か否かを判定するモデルを作成する手法が紹介されていたのでやってみた

    環境

    • google colabratory

    イジングモデルの計算とシミュレーション方法

    理論、方法ともに”ディープラーニングと物理学 原理がわかる、応用ができる”より。結構いろんな章を参考にした

    ページ数は参考にした箇所を表す

    ハミルトニアンと確率

    p. 48~

    ハミルトニアンは系におけるエネルギーのようなもの

    熱浴系においてエネルギーEを持った状態が実現される確率は

    p=1Zexp⁡[−EkBT]p = \frac{1}{Z}\exp[-\frac{E}{k_BT}]

    kBk_Bはボルツマン定数、TTは温度[K]を表す

    Zは分配関数といい、状態確率の規格化定数のようなもの。以下のように表す

    Z=∑全状態exp⁡[−HkBT]Z = \sum_{全状態}\exp[-\frac{H}{k_BT}]

    メトロポリス法

    p.126~

    確率的シミュレーションにおいて、状態遷移をある条件で行っていく方法のこと 状態遷移はエネルギーとその遷移確率から決まっていく

    平衡分布を以下のように取る

    peq(si)=1Zβe−βH[si]p_{eq}(s_i) = \frac{1}{Z_{\beta}}e^{-\beta H[s_i]}

    β=1kBT\beta=\frac{1}{k_{B}T} は逆温度、sis_iはある状態、H[si]H[s_i]はハミルトニアン表す

    iiからjjに行く確率を求める

    H[si]<H[sj]H[s_i] < H[s_j] となるとすると、sis_iはsjs_jよりも低いエネルギーなので、iに留まりそう。これを

    p(si∣sj)=1p(s_i|s_j) = 1

    とおく

    詳細釣り合いの原理(iからj、jからiに行く確率はどちらも等しい)より反対方向には

    e−βH[sj]=p(sj∣si)e−βH[si]e^{-\beta H[s_j]} = p(s_j|s_i) e^{-\beta H[s_i]}

    ここで左辺はp(si∣sj)=1p(s_i|s_j) = 1、より

    p(sj∣si)=e−β(H[sj]−H[si])p(s_j|s_i) = e^{-\beta (H[s_j]-H[s_i])}

    となり、状態遷移確率は各状態のエネルギー差分に依存する（エネルギー差分が低いほど、高温ほど高い確率）

    すなわち、ある状態を変化させて、その時のエネルギーの変化をみていくことで 状態の遷移確率がわかる

    メトロポリス法は以下のような順番で行う

    1. 適当な初期状態iを用意
    2. 状態iでのハミルトニアンを求める
    3. 状態をiからjに変化させる（変化させる手法は任意
    4. 状態jでのハミルトニアンを求める
    5. 状態の更新を行う。メトロポリステストと呼ぶ。

    エネルギーが小さくなるH[si]>H[sj]H[s_i] > H[s_j]ならば次の状態をjに更新する。そうでなければ、遷移確率で判定を行う プログラミング的には0~1の乱数rに対してr>p(sj∣si)r>p(s_j|s_i)ならば状態を更新する 状態が更新されることをacceptという、反対にそのままのときはrejectという

    イジングモデルのシミュレーション

    イジングモデルは磁性体をミクロな視点から説明するモデルのこと

    各格子点に±1\pm{1}の値をとるスピンsが配置されており、それらの配位（各スピンの状態）より系のハミルトニアンが求まる

    二次元正方格子を考える。あるスピン配位でのハミルトニアンは以下のように表される

    H[s]=−J∑i,jsi,j(si+1,j+si,j+1)H[s] = -J\sum_{i,j}s_{i,j}(s_{i+1,j}+s_{i,j+1})

    スピンiiのハミルトニアンは隣接しているスピンの状態に依存する

    Hi=−Jsi∑j∈<i,j>sjH_i = -J s_i \sum_{j \in <i,j>}s_j

    <i,j><i,j>はiに隣接しているスピンの集合

    状態変化はあるスピンの反転とする。変化前後のエネルギー差分と状態遷移確率より、メトロポリス法をもちいて状態の更新を行っていく

    各ステップで状態変化を行い、エネルギーHとスピン配位s（配列）を取得する また、相転移の温度を閾値としてラベルを設定する。ある温度Tについて、T<2.27T<2.27ならばd=0d=0、T>2.27T>2.27ならばd=1d=1とする（T=2.27T=2.27のときはd=0d=0とした） ある温度における、ある時点のスナップショットを取得して、(温度範囲×取得するスナップショット数)分、(step, T, H, s, d)の学習データを作成する

    • メトロポリステストに用いるハミルトニアンの変化HdiffH_{diff}の計算方法

    ある点si,js_{i,j}において、スピンを反転させる（s→s′s \rightarrow s'）とき

    Hdiff=Hj−HiH_{diff} = H_j - H_iを求める。si,js_{i, j}以外は変わらないので

    Hi=−Jsi,j(si−1,j+si+1,j+si,j−1+si,j+1)H_i = -Js_{i, j}(s_{i-1, j} + s_{i+1, j} + s_{i, j-1} + s_{i, j+1}) Hj=−Jsi,j′(si−1,j′+si+1,j′+si,j−1′+si,j+1′)H_j = -Js'_{i, j}(s'_{i-1, j} + s'_{i+1, j} + s'_{i, j-1} + s'_{i, j+1})

    ()内、周囲スピンの和は

    sadj=si−1,j+si+1,j+si,j−1+si,j+1s_{adj} = s_{i-1, j} + s_{i+1, j} + s_{i, j-1} + s_{i, j+1}

    と置き換えられ、以下のように求まる

    Hdiff=(−Js′sadj)−(−Jssadj)=−J(s′−s)sadj=−2Jsi+sadjH_{diff} = (-Js's_{adj}) - (-Jss_{adj}) = -J(s' - s)s_{adj} = -2Js_i + s_{adj}

    実装

    pythonで実装した。gistを置いておく

    シミュレーションで得られたスピン配位に対して、相転移前、後かどうかを学習させて、モデルを作成した

    Sorry, something went wrong. Reload?
    Sorry, we cannot display this file.
    Sorry, this file is invalid so it cannot be displayed.
    view raw ising_cnn.ipynb hosted with ❤ by GitHub

    結果

    シミュレーション

    各温度の特徴をみてみる

    温度とエネルギーの関係みると、閾値辺りでなにかが変化がありそう

    T vs. H

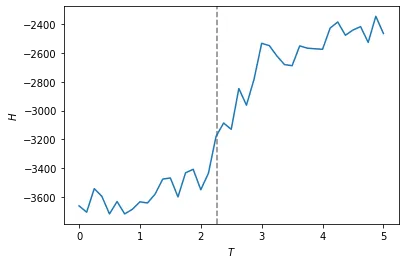
    また、各温度でのスピン配位をみると、閾値より低いか高いかで構造に特徴がありそう

    T=0 T=2.5 T=5.0

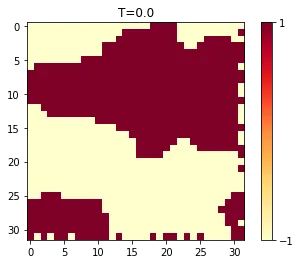
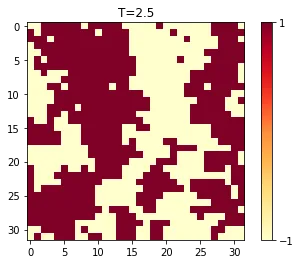
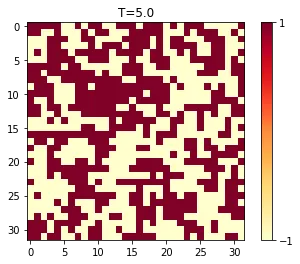
    CNN

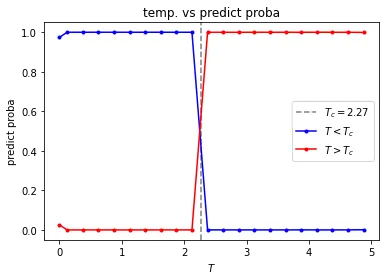
    各温度に対するデータの予測確率をプロットすると閾値で確率が変化している。すなわちあるスピン配位から相転移点を特定できるような機械学習モデルができているといえる

    プロット自体は本のp. 193の図を真似てつくった

    T vs. predict proba

    参考

    手法周り

    • ディープラーニングと物理学 原理がわかる、応用ができる

    python周り

    2022, Built with Gatsby. This site uses Google Analytics.