causalmlのT-learnerでATEを算出

2020/02/29machine-learning python causalml ate

causalmlを試した。岩波データサイエンス vol.3に載っていたデータを使って、平均処置効果とアウトカムの推定に用いた特徴量のimportance等を出してみた

機械学習モデルを用いてアウトカムを推定し、平均処置効果(average treatment effect, ATE)を算出してみた。causalmlのモジュールにて各々featureのimpotanceも表示、可視化することができたので試してみた

環境

python: 3.6.9
causalml: 0.7.0

データ

データは岩波データサイエンス vol.3 p91~の章にて使用されていた、テレビCM接触有無とスマートフォンにおけるゲームアプリ利用のデータを用いる

CMの広告効果を測定するためのサンプルデータになっている。データ(csv)はこちら

手法

手法はT-learnerを用いた。causalmlのドキュメントより

平均アウトカム $\mu_0, \mu_1$ の推定を統制群、処置群に対して作成した機械学習モデルを用いて行う

$\mu_0(x) = E[Y(0)|X=x]$

$\mu_1(x) = E[Y(1)|X=x]$

$x$ は特徴量を、 $Y$ はアウトカムを表す。各々統制群と処置群について推定している

CATE(Conditional Average Treatment Effects Estimation)の計算

$\hat{\tau} = \hat{\mu}_1(x) - \hat{\mu}_0(x)$

として、介入効果 $\tau$ の推定値を求める

ATEにC(conditional)がつくのは、特徴量 $X$ の元でという、条件をおいているところからくるらしい

実装

岩波データサイエンス vol.3の例と同じように、CMの閲覧有無に対するゲームプレイ時間への効果をみてみる

cm_dummyを介入効果
gamesecondをコンバージョン(アウトカム)

として分析していく

データ読み込み

from causalml.inference.meta import XGBTRegressor

import pandas as pd
import numpy as np

# load data for game cm
df = pd.read_csv('https://raw.githubusercontent.com/iwanami-datascience/vol3/master/kato%26hoshino/q_data_x.csv')
df.head()

単純比較による効果の確認

単純にCM閲覧有無でのゲームプレイ時間の違いをみてみる

# treatmentでcvは異なる？
df.pivot_table(
               values=['gamedummy', 'gamesecond'],
               index='cm_dummy',
               aggfunc=[np.mean, np.size],
               margins=True)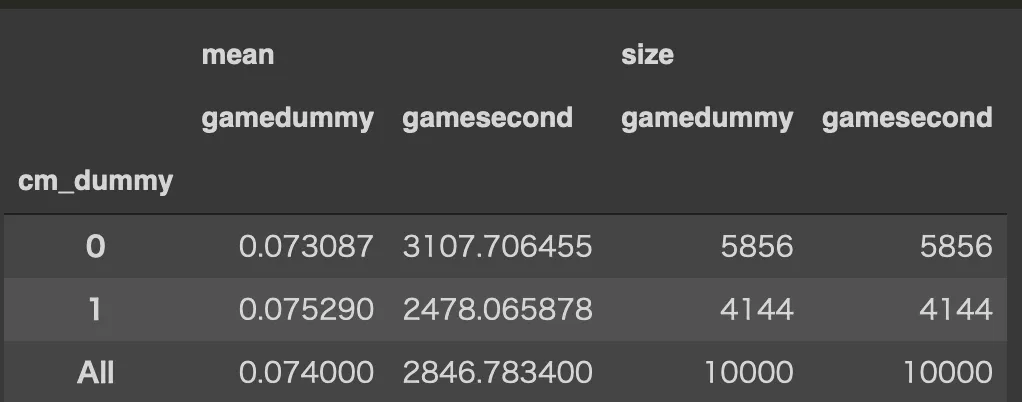

print('単純比較によるCM閲覧有無のゲーム時間(s)の効果: %d' % (2478 - 3107))
print('単純比較によるCM閲覧有無のゲームプレイ有無の効果: %f' % (0.075290 - 0.073087))

単純比較によるCM閲覧有無のゲーム時間(s)の効果: -629
単純比較によるCM閲覧有無のゲームプレイ有無の効果: 0.002203

CMをみるとプレイ時間は少なくなる、という結果になっている。本文中でも触れられているがCM接触者とCM非接触者間にはそもそも、集団として差がある。CMに接触しやすい人はテレビよく見ている層、例えばあまりゲームをしない高齢層だったり、ゲームするよりテレビをみる時間が長い人が多い、といった偏りが存在すると予想される

このようなサンプルセレクションによるバイアスがあるため、広告をみると効果がなくなる、といった直感に反した結果になっている。以下でこのバイアスを補正した効果を推定してみる

学習データ準備&causalmlによる機械学習モデルの作成

特徴量として、target segmentは削除

gamecount gamedummy

も共変量になりそうなので削除

また、特徴量は岩波データサイエンス本と同じものを使う

df_feats = df.drop(['cm_dummy', 'gamedummy',
                    'gamesecond', 'gamecount', 'T', 'F1', 'F2', 'F3', 'M1', 'M2', 'M3',
                    'job_dummy8', 'fam_str_dummy5'
                    ], axis=1)

is_treat_list = np.array(list(df['cm_dummy']))
is_cv_list = np.array(list(df['gamesecond']))

X = df_feats.values
# gemasecondをアウトカムとして使う
y = np.array(list(df['gamesecond'].astype(int)))
#y =  np.array([1 if c else 0 for c in is_cv_list])
treatment = np.array([1 if t else 0 for t in is_treat_list])
xg = XGBTRegressor(random_state=41)

te, lb, ub = xg.estimate_ate(X, treatment, y)

print('Average Treatment Effect (XGBoost): estimate {:.4f}, lower bound {:.4f}, upper bound {:.4f}'.format(te[0], lb[0], ub[0]))

Average Treatment Effect (XGBoost): estimate 907.1362, lower bound 472.6813, upper bound 1341.5911

平均処置効果は907(s)と推定され、CMをみるとゲームプレイ時間は907秒伸びるという効果があったと結論できる(本より効果量が小さいのは手法が異なるからだろうか)

特徴量の重要度、寄与度のplot

介入群かどうか(以下では、1と表示されてる)の推定における特徴量の重要度等もcausalmlのモジュールで簡単にplotすることができる

xg.plot_importance(X=X,
                         tau=xg.fit_predict(X, treatment, y),
                         normalize=True, 
                         method='auto', 
                         features=df_feats.columns,
                         random_state=42)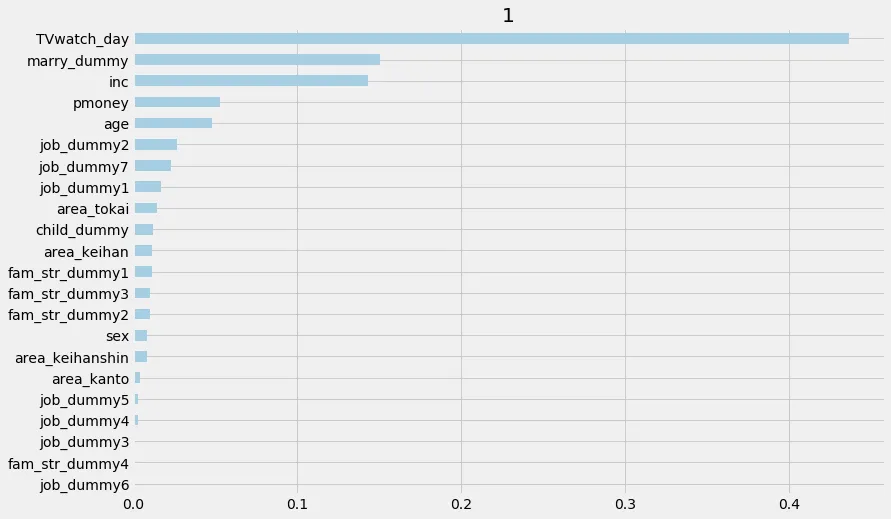

permutationもplotできる

xg.plot_importance(X=X, 
                         tau=xg.fit_predict(X, treatment, y),
                         method='permutation',
                         features=df_feats.columns,
                         random_state=42)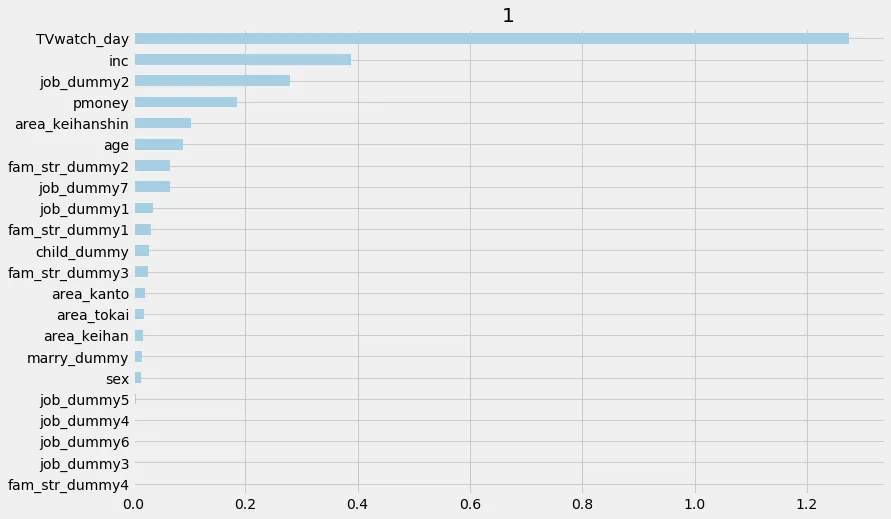

また、特徴量の推定値への寄与度もshapを用いて可視化することができる

xg_shap = xg.get_shap_values(X=X,  tau=xg.fit_predict(X, treatment, y))
xg.plot_shap_values(shap_dict=xg_shap, features=df_feats.columns)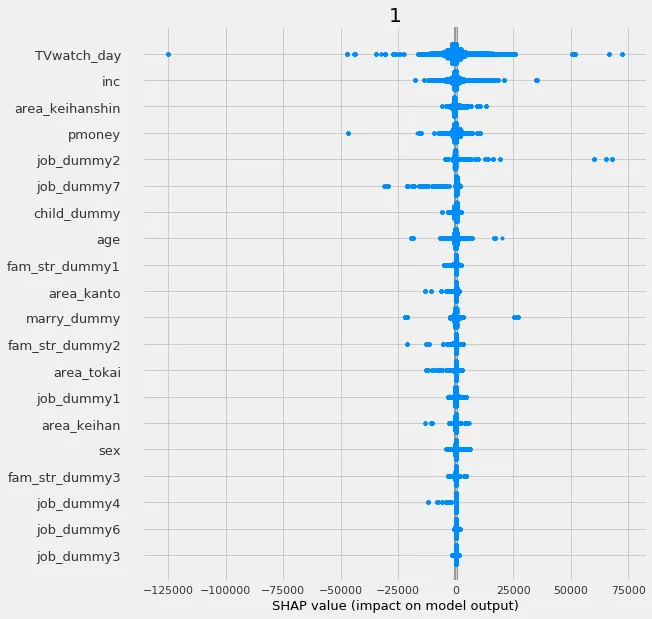

job_dummy2

は何やら正の方向に寄与する様子

ある特徴量に絞ってplotすることもできる

# interaction_idx set to None (no color coding for interaction effects)
xg.plot_shap_dependence(treatment_group=1,
                              feature_idx='TVwatch_day',
                              X=X,
                              tau=xg.fit_predict(X, treatment, y),
                              interaction_idx='inc',
                              features=df_feats.columns,
                              shap_dict=xg_shap)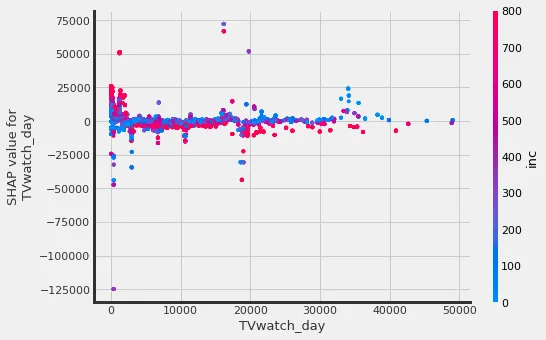

TVをみる時間が少ない人の方がshapの値が高い（正の方向への寄与度が高い）。また、TVを割と長時間見ていて、年収高いほどCMに接触しないような傾向がみて取れる

コード全体はgistにした

gist:uni-3/8689cad965447e0e04ca896c5b694669

所感

データの準備、結果の読みときに苦労した(共変量を外さずモデルを作ってしまい、効果量が0になってしまったり、shap等のestimateの解釈が難しかった)。機械学習と効果測定、ドメイン知識など、いろいろな分野の知見がないとなかなか分析が難しそうだな、と思った

参考

岩波データサイエンス Vol．3
https://github.com/uber/causalml/blob/master/examples/feature_interpretations_example.ipynb 参考にしたノートブック
https://orizuru.io/blog/machine-learning/shap/ shapの説明
https://blog.amedama.jp/entry/permutation-importance permutation impotanceの説明
https://tjo.hatenablog.com/entry/2016/08/29/190000 傾向スコアによる効果の解説等を参考にした