pymc3を用いてベイズ統計によるABテスト結果検証用notebookを作った

いわゆるベイジアンABテスト。流行ってそうなので、挑戦してみた。 統計モデルをつくる作業はあまりやったことがなかったので、面白かった

環境

• python: 3.7
• pymc3: 3.8

実験

図の見方と流れを書いておく。コードは最後にgistを掲載する

ABテストとして、例えばレコメンドロジックについて実装Aと実装Bを試したとする

どちらのロジックが優れていたか、各々のimpressionとconversionの値を用いてconversion rateの比較することを考える

データとしては以下のようになった

Bの方が良さそうだが、本当に差分があるかどうかをベイズ統計を用いて評価してみる

# sampla data
sample_a = 6746
cv_a = 972
sample_b = 6790
cv_b = 1200

pymc3を用いて以下のようなモデルを設定し、パラメータを推定する 事前分布としてベータ分布を用いる(alpha bata が1のときは一様分布となる) 事後分布はベルヌーイ分布とする

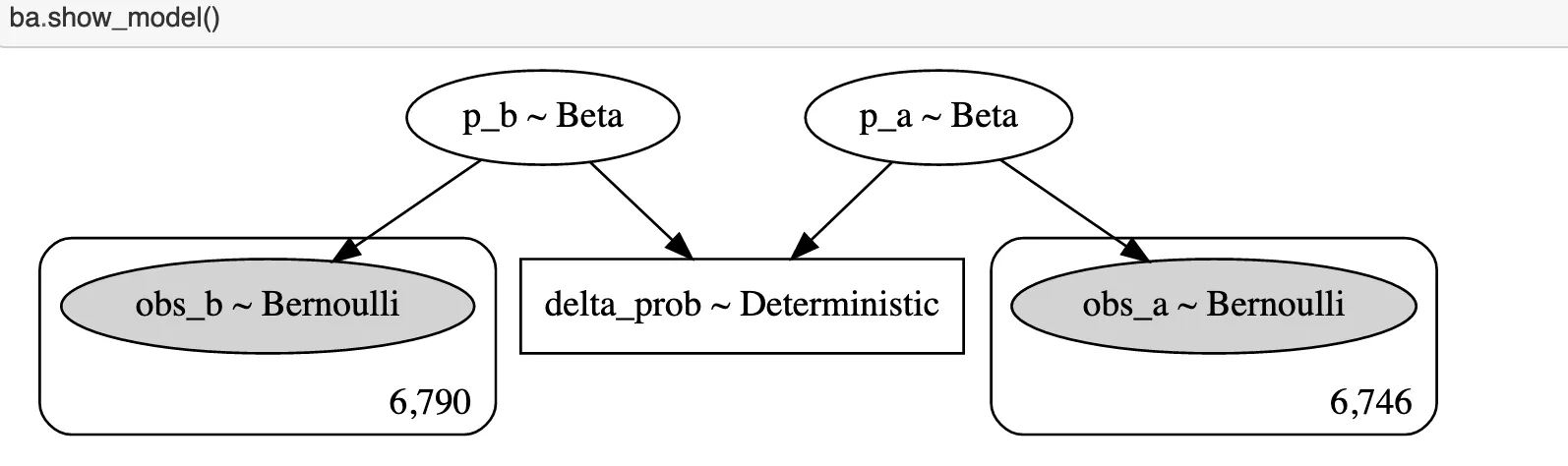
ba = BayesianAB(sample_a, cv_a, sample_b, cv_b)
ba.fit_model(n_samples=10000)

推定結果は以下のようになった

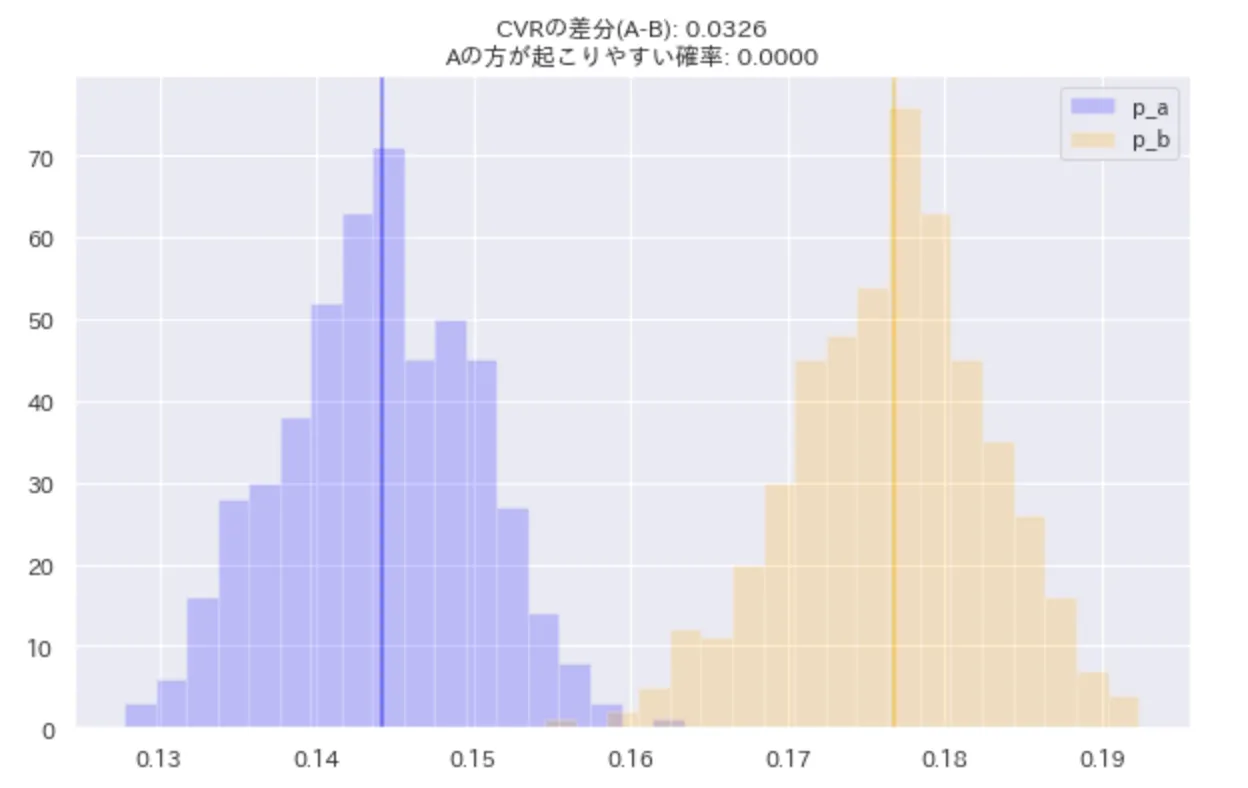
r_hatが1に近いので、シミュレーション自体は収束してそう

また、Aの方が起こりやすい（Aの方が大きい値になりやすい）確率は0であり、Bの方がCVも3%ほど高く、有意差もある。図からも明らか

コード全体はgistにした

gist:uni-3/ec988d24406b2d4f53ea8e6ee6d5b281

まとめ

ABテストにて有意差を評価する時には基本的にt検定を用いた平均の差の検定を用いることが多いが、こちらの方法は、サンプルサイズが大きい(数千程度)と、必ず有意差ありと出てしまうらしい。

ベイズ統計を用いることで、図で表せるためわかりやすい＋サンプルサイズをあまり気にしなくて良いので、便利に使えそうだと思った

参考

• A/Bテストの評価をベイズ統計でやってみない？ - tdualのブログ
  数式周りから実装まで参考になった

• PyMC3を使ったベイズ推論によるA/Bテスト - ZOZO Technologies TECH BLOG

• Pythonによるベイズ統計モデリング: PyMCでのデータ分析実践ガイド
  pymc3の使い方を参考にした